Función Cuadratica: febrero 2012

En matemáticas, una función cuadrática o función de segundo grado es una función polinómica definida como:

Gráficas de funciones cuadráticas.

$f(x) = ax^2 + bx + c \,$

en donde a, b y c son números reales (constantes) y a es distinto de 0.

La representación gráfica en el plano cartesiano de una función cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las ordenadas. La parábola se abrirá hacia arriba si el signo de a es positivo, y hacia abajo en caso contrario. El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico

La derivada de una función cuadrática es una función lineal y su integral una función cubica.

En la ecuación cuadrática sus términos se llaman:

Si la ecuación tiene todos los términos se dice ecuación completa, si a la función le falta el término lineal o independiente se dice que la ecuación es incompleta.

Ceros o Raíces de la Función Cuadrática

La función cuadrática, como toda función puede tener "ceros" o "raíces", que son valores de la variable independiente "x" que hacen cero a la función "y"

Esta fórmula nos permita hallar las dos raíces o ceros de la ecuación cuadrática, lo que se logra al tomar alternativamente los signos "+" y "-" de la formula resolverte.

Como vemos, una parábola puede tener dos ceros reales y distintos como en este caso, en que corta dos veces en su trayectoria real al eje "x", en los puntos x1 y x2.

Tipos de soluciones de la Ecuación de segundo grado

El radicando de la formula resolvente, llamado discriminante determina el tipo de soluciones que tiene la ecuación de segundo grado.

1) Si el discriminante es positivo: La raíz cuadrada de un número positivo es también positiva, con lo cual el doble signo de la raíz cuadrada lleva a dos raíces reales y distintas. La curva cortará entonces dos veces en su trayectoria real al eje "x".

2) Si el discriminante es cero: La raíz cuadrada de cero es cero, con lo cual el doble signo de la raíz cuadrada lleva a dos raíces reales e iguales, o puede decirse una raíz real doble. La curva tocará entonces una sola vez al eje "x" sin atravesarlo. Puede verse que la curva "rebota" sin cruzar el eje de abscisas, o sea que tiene su vértice sobre dicho eje.

3) Si el discriminante es negativo: La raíz cuadrada de un número negativo no tiene resultado en el campo real, con lo cual la solución son dos raíces complejas conjugadas. La curva no toca en este caso al eje "x" sino que se halla siempre por arriba o por debajo de dicho eje de abscisas.

El vértice

Es el punto de ordenada mínima si la parábola abre hacia arriba, y es el de ordenada máxima si abre hacia abajo.

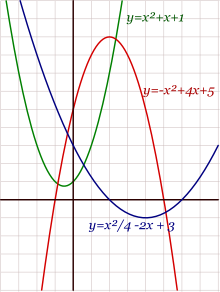
En general, si una función cuadrática tiene la expresión $\begin{displaymath}f(x)=ax^2+bx+c\;,\end{displaymath}$ las coordenadas del vértice de la parábola correspondiente son: $\begin{displaymath} \left(\frac{-b}{2a},c-\frac{b^2}{4a}\right) \end{displaymath}$
Ejercicio:Comprueba que los vértices de las cuatro parábolas dadas corresponden a los puntos dados, haciendo el cálculo de las coordenadas $\begin{displaymath}\left( \displaystyle \frac{-b}{2a},c-\displaystyle \frac{b^2}{4a} \right)\end{displaymath}$ en cada caso.
Los puntos de corte con los ejes.Con el eje de las ordenadas hay un solo punto de corte. No puede haber más de uno cuando la parábola representa a una función cuadrática, puesto que el punto de corte con el eje de las ordenadas es el punto cuyas coordenadas son . Entre las propiedades de una función está la que asegura la unicidad de la imagen de cada elemento. Por ejemplo, en la función (1), , el punto de corte con el eje de las ordenadas es , donde $\begin{displaymath} f(0)=2(0)^2+0-3=-3 \end{displaymath}$ es decir, es el punto .Este punto está muy cerca del vértice, pero no coincide con él. En la función (2), , el punto de corte con el eje de las ordenadas sí coincide con el vértice, pues $\begin{displaymath} f(0)=3 \end{displaymath}$ y por lo tanto el punto es